Sextant Errors And Corrections

Sextant Error

The sextant is a high precision instrument. As such it is to be handled with care as shocks can easily damage or alter its characteristics. When delivered new, it should be accompanied by a calibration certificate which specifies the reading error along its full scale. The arc covered by the lever is slightly over 60 degrees (hence the name sextant). And since the angle measured is twice that, the range of measurement is 120 degrees.
The correction sheet should show errors lower than 0.1' of arc at all points along the arc (if it is not, then buy another sextant) except for a constant permanent offset which is adjustable but never actually 0 unless you are very lucky.

This offset error can be checked easily by sighting on a distant object (a bright star is strongly suggested, one can't find much further objects than these), or instead use the horizon. Adjust the cursor until the object and its mirror image are superimposed. The reading is the sextant permanent error. In the tradition of the old navigators, we say the error is "Off the arc" if negative (the sextant is reading low) and the error must be added to the reading. Or the error is "On the arc" (the sextant is reading high) and the error must be subtracted from the reading.

Why take a distant object? Well the image seen from the mirror and the direct image are about 150 mm (6 inches) apart and sighting on a not too distant object will cause a parallax error. If you don't want to use a star, at least use the sea horizon which is a few kilometers away.

Corrective terms

Now this is all very straightforward except for the fact that the sextant altitude is always wrong. Apart from the sextant error itself, which is always the same and the easiest to allow for, there are 5 other measurement errors which require compensation

  1. First and most obvious, the horizon that you use is not parallel with the surface of the earth under you feet. and the higher up you are, the greater the error (because the further away is the horizon). Consequently, the measurement that you take is always larger than it should be. The formula to correct for this error depends on the height of the eye above the surface of the sea. Unless you use a bubble sextant, in which case there is no error, but I defy anyone to use a bubble sextant on a small boat, with the boat motion, the bubble would appear to suffer from St Vitus's Dance.

    This effect is called "The dip of the sea horizon" and is equal to:

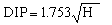
    Where H is the height of eyes in metres, and DIP is the correction in minutes of arc.
    This correction is always subtractive.

  2. Second, less obvious but just as important is the refraction effect of the atmosphere. This effect, like the dip, always makes the reading larger than it would be if the atmosphere did not exist. The effect is larger for low altitudes (reaching about 30' of arc horizontally. Since the sun has an apparent diameter of about 32' of arc, when we see it just reaching the horizon at sunset, in fact, in reality it has just disappeared, only the refraction effect makes it still visible to us). The atmospheric pressure and the temperature of the air affect this refraction to some degree, in fact, the effect is proportional to the air density and the following formula is the one I use for compensation:

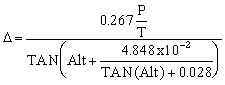
    The correction is in minutes of arc (and always subtractive)

    P is the atmospheric pressure in millibars,
    T is the air temperature in degrees Kelvin
    Alt is the altitude in degrees.

    This formula has been checked against the published figures in the Admiralty's Almanac, Brown's Almanac and Norie's tables. The agreement is better than 0.01' of arc for all altitudes between 7 and 90 degrees. and better than +/- 1' of arc between 7 and 0 degrees.

  3. Thirdly, when observing the sun or the moon, it is impossible to judge accurately where the center is, what navigators do is make one edge just touch the horizon, which edge it is depends on personal preferences and also the contrast (one may be easier to see than the other), the edges are called "limbs" in technical jargon, hence we talk of the sun lower limb, or the moon upper limb.The published tables in the almanac apply to the centre of the object, therefore if using the lower limb, you need to add 1/2 the diameter of the sun (or moon) to your measurement. Vice versa, if using the upper limb, you need to subtract a 1/2 diameter. the apparent size of the object will vary somewhat over the year , the 1/2 diameter values for the sun are listed at monthly interval, for the moon daily.

  4. Fourthly, the parallax error needs to be compensated for. For the sun , the error is always less than 1' of arc and not worth bothering about, (all the other effects are imprecise, and with the boat moving constantly, just be lucky to get an answer within 2 or 3'). But if you use the moon, the effects can be quite large (almost as much as 1 degree). The parallax error is because the tables assume that the observer is at the centre of the earth. This means that an observer seeing the moon with its centre on the horizon (after allowing for the refraction correction) would be wrong to assume 0 degree since it means the angle is really the earth radius divided by the distance from the moon to the earth. This value is also published in the almanac under the name of HP (Horizontal parallax, not "Hewlett-Pakard"). The method is to first do the dip and refraction corrections to the measurement, call this the Observed Altitude (OA), then add HPxCOS(OA) to it. This correction is always additive as the angle measured from the surface of the earth is always less than that which would be seen from the centre.

  5. Last, and also for the moon only, one may wish to compensate for "the augmentation of diameter" effect. this is due to the fact that the published 1/2 diameter is as seen from the centre of the earth. It is still valid when the moon is just rising or setting, but when it is close to overhead, the distance from us to the moon has been shortened by the radius of the earth. this causes the moon to appear slightly bigger than the published figure. (the maximum effect is about 0.3' of arc and I personally wouldn't bother with it). However, for the masochists among you, here is the corrective term:

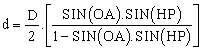
    Note also that there is a relation linking the moon 1/2 diameter and the horizontal parallax : D/2 = 937 SIN(HP).

In Practice

If using sight reduction tables, like HO249 or whatever the name of the newer ones is. You will notice that the tables are tabulated for LHA varying in 30' increments. Similarly , the latitudes are also varying in 30' increments. When choosing your DR, since it is likely to be wrong in any case, then choose one with a latitude being an exact multiple of 30', and a longitude which when subtracted from the GHA of the celestial object, will also yield a LHA also a multiple of 30'. This way the interpolations are reduced to the minimum required.

Avoid using the moon, as you can see from above, it requires all sorts of corrections. Not a good thing if you are under pressure.

Another little detail to be aware of is when the declination of the sun changes sign, it is easy to miss it and keep thinking it is North when it is in fact south. Highlight your almanac when you first buy it so when you get to that particular page (March and September) the colouring will spring to your attention.

Learn to know the stars, they are easy to recognise, and the main ones are almost all in the plane of the ecliptic. Sirius (canis major) is so bright that if you know where to look, you can see it when it is still day light. So is Canopus. But even constellation such as Orion (the saucepan is what Australians commonly call it) can be useful, the 3 dimmer stars inside the square are straddling the equator, this means that no matter where you are on earth, the stars always rise exactly east and set exactly west, pretty handy to check what the compass error is. Besides stars are pretty and we should spend more time looking at them.

Celestial Navigation back next Rhumb Line Formulas